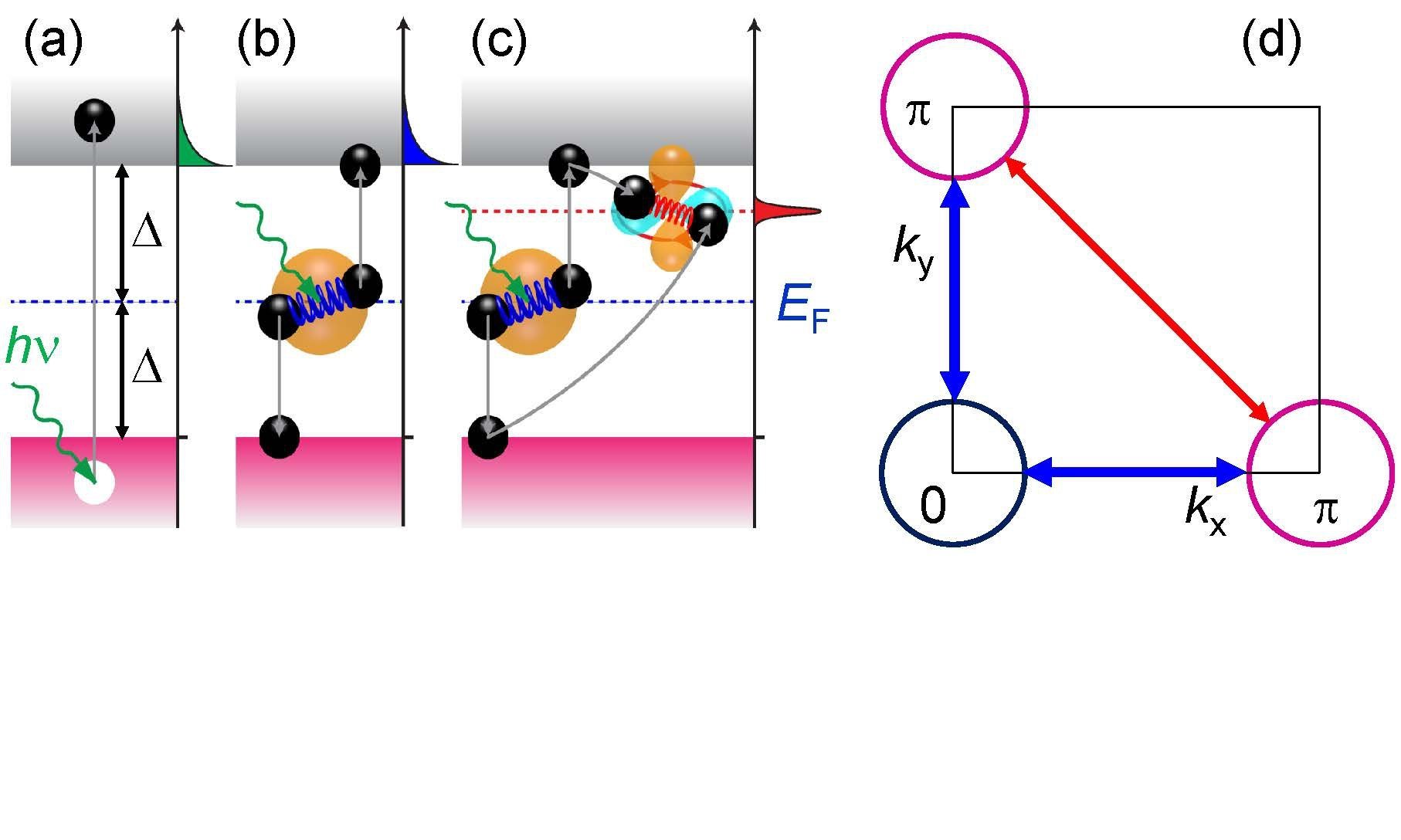
In a superconductor, the excitation of electron-hole pairs requires a minimal energy of 2Δ between incoming and outgoing photons (a). In a second process, Cooper pairs, which are responsible for the infinite conductivity, are broken up for energies exceeding 2Δ (b). Thus, Raman scattering allows one to determine the condensation energy Δ of a superconductor. If the gap depends on the momentum k of the electrons such as in the cuprates or the iron-based materials, the selection rules allow one to map out Δ_k in momentum space. Panel (d) shows the interactions possible in a prototypical ferro-pnictide. The circles represent the approximate shapes of the Fermi surface sheets. The horizontal and vertical blue arrows symbolize the ground state interaction responsible for Cooper pairing. The diagonal magenta line represents an additional interaction between two other Fermi surface sheets. Since it is weaker than the ground state interaction, it leads “only” to a bound state inside the gap (c). These modes, although predicted a long time ago, were unambiguously observed and explained only in the pnictides. These “dancing electrons” strongly support unconventional Cooper pairing in this material class driven by spin fluctuations rather than phonons as in conventional superconductors.