Quantum Theory
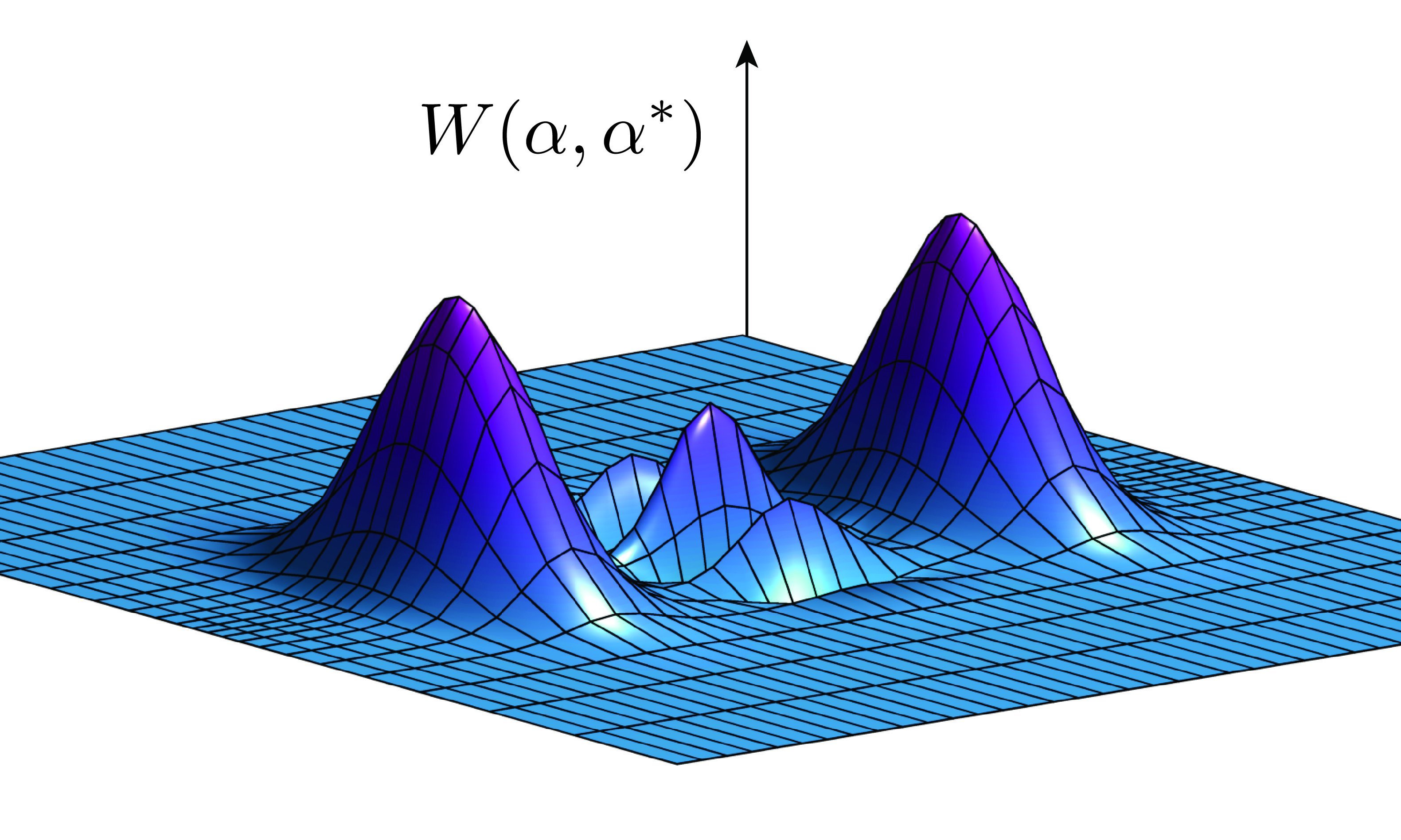
The development of laser cooling and trapping techniques for atoms in the previous century enabled us for the first time to study and fully control individual quantum systems in the lab. Apart from progressively refined tests of the laws of quantum mechanics, these capabilities also provide us with the basis for new, quantum-enabled technologies, such as quantum computers, quantum simulators or enhanced sensors. In recent years, a similar level of control has now also been achieved for artificial macroscopic quantum systems, such as superconducting quantum circuits or micro- and nanomechanical resonators. Unlike atoms, the properties of those systems can be engineered and designed with great flexibility and scaled-up using established nanofabrication techniques. This offers many intriguing new possibilities for quantum technology applications and for exploring complex quantum phenomena under previously inaccessible conditions.
Our theory efforts are focused on the analysis of control and manipulation techniques for engineered solid-state quantum systems. One of our primary goals is to develop more efficient quantum information processing schemes and robust protocols for operating scalable quantum networks. With a detailed modelling and numerical simulation of such processes, we support and complement the ongoing experimental activities at the WMI in this direction, but also strive to identify and tackle some of the future challenges that implementations of large-scale quantum information processing infrastructures will naturally bring about.
Beyond their potential use for quantum-technology applications, a particular interest in these artificial systems arises from their unique possibilities to engineer both coherent and dissipative interactions at the quantum level and to design model systems and interaction parameters almost at will. These features allow us to explore new physical effects and phenomena that are otherwise not encountered in nature. In this context, we are specifically interested in light-matter interaction effects in 1D waveguides and in the so-called ultrastrong coupling regime, where the coupling strength between a single atom and single photon exceeds the bare energy of that photon. While such conditions are not accessible with real atoms, they can be realized with ‘artificial’ atoms, i.e., superconducting two-level systems, coupled to microwave photons. From a theoretical perspective, the analysis of such systems is particularly challenging since many of the usual approximations and simplification are no longer applicable and new analytic and numerical approaches must be developed.
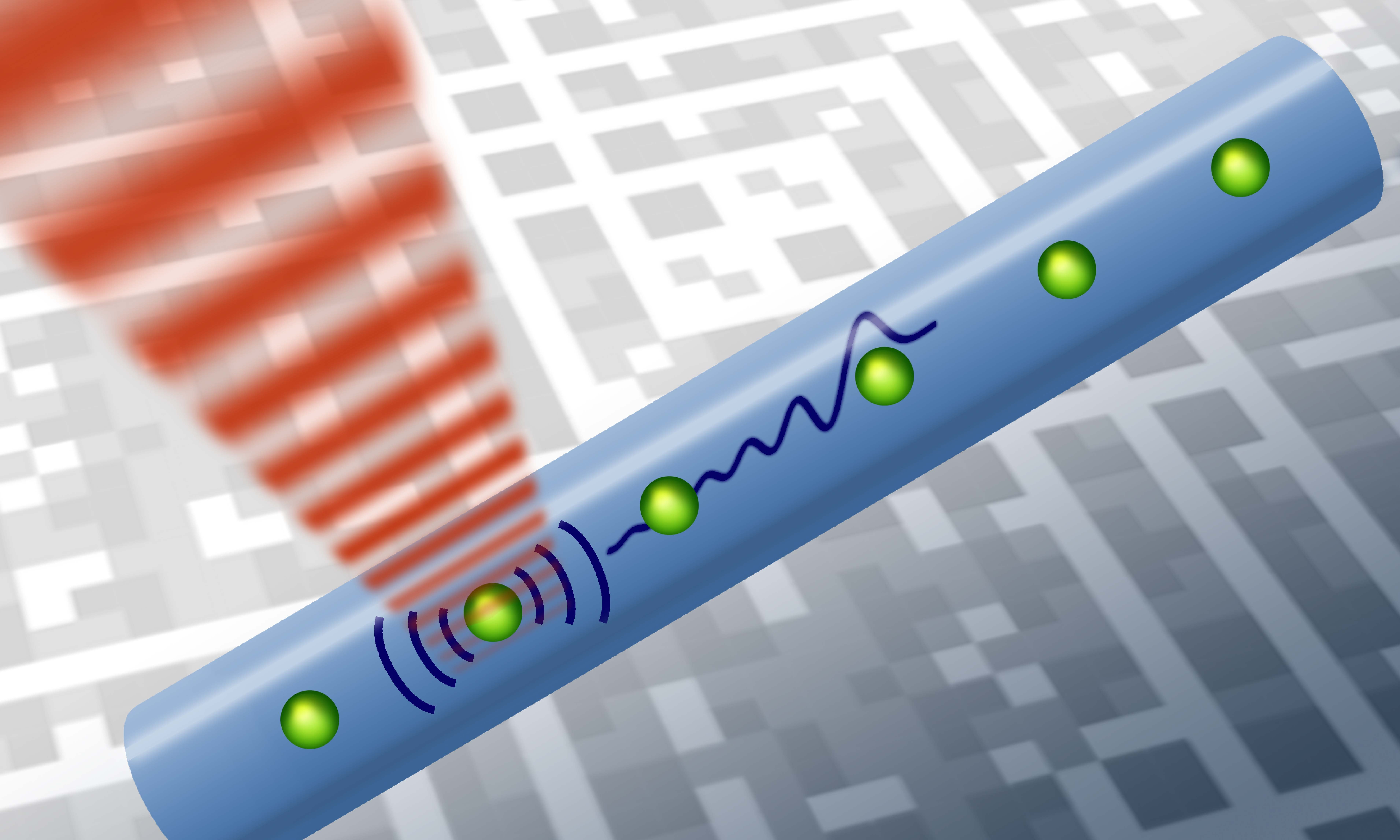
The distribution of entanglement between separated nodes of a quantum network is a fundamental task for almost all quantum communication and quantum information processing applications. While optical photons are the only way to distribute quantum states over very large distances, for on-chip communication also microwave photons or even propagating phonons, i.e., quantized sound waves, can be used for this task. Our goal is to find more and more efficient ways to interface these information carriers with stationary superconducting qubits or spin-based quantum memories and to develop new protocols for a fast and robust distribution of entanglement across large-scale quantum networks.
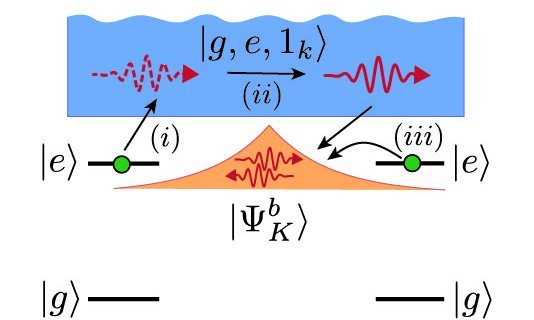
Compared to free space, the interaction between light and matter can become considerably more involved when atoms or other emitters are coupled to structured electromagnetic environments such as 1D waveguides or 2D photonic lattices. Under such conditions the strong confinement and restricted propagation direction can give rise to effective infinite-range interactions between the emitters, correlated decay processes or the formation of atom-photon bound states. In 2D systems, additional engineering tricks can be used to create synthetic magnetic fields for light, which gives rise to even more exotic forms of chiral light-matter interaction effects.
Quantum electrodynamics (QED) is the fundamental theory for charges interacting with the electromagnetic field. QED is a weakly interacting theory, as evident by the smallness of the finestructure constant. In quantum optics or solid-state physics, it is exactly this property that allows us to model light-matter interactions in terms of well-defined photonic and atomic excitations on top of a trivial vacuum state. However, with recent advances in the field of circuit QED it is now possible to go beyond this well-established paradigm. In these systems, the effective coupling between a single artificial atom (a superconducting qubit) and a microwave photon can even exceed the energy of the photon itself. From a more general perspective, such conditions can be interpreted in terms of an effective finestructure constant of order unity and give rise to many questions related to the general structure of light-matter interactions in a strongly-interacting, i.e., non-perturbative theory of QED.
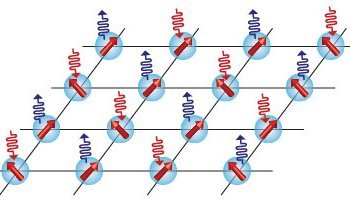
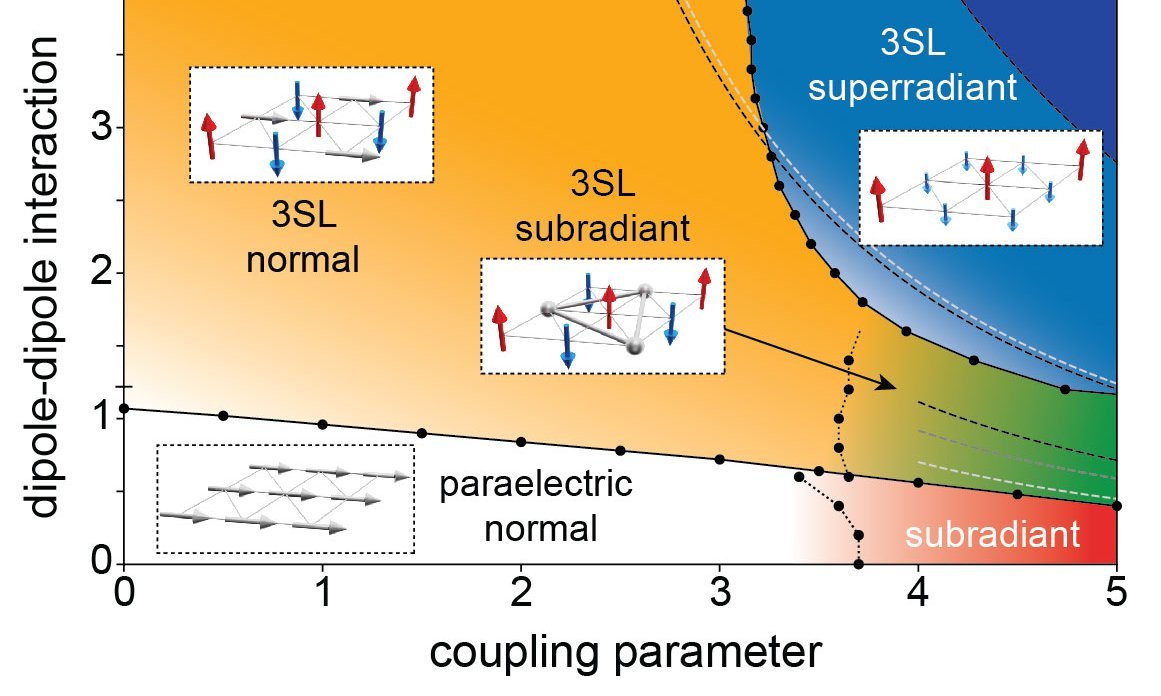
While the theory of phase transitions in ground and equilibrium states of condensed matter systems is well established, comparably little is still known about the critical behavior of driven-dissipative many-body systems out of equilibrium. Such conditions occur for example, in interacting quantum optical systems or superconducting circuits, which are naturally subject to decay while being externally driven by lasers or microwave fields. Many-body problems out of equilibrium are essentially impossible to simulate with conventional numerical methods and new efficient analytic and numerical approximation methods are required to treat such problems. Beyond the development of such methods, we are also interested in new physical phenomena that arises in open quantum systems, ranging from quantum PT-symmetry breaking to non-equilibrium phase transitions in microscopic power grids.
